قانون حجم متوازي المستطيلات بالمراجع
قانون حجم متوازي المستطيلات بالمراجع، يُعرّف الحجم بأنه مقدار المساحة أو المادة في شكل ثلاثي الأبعاد، ويتم قياس الحجم بالمتر المكعب وفقًا لنظام الوحدة الكلي.
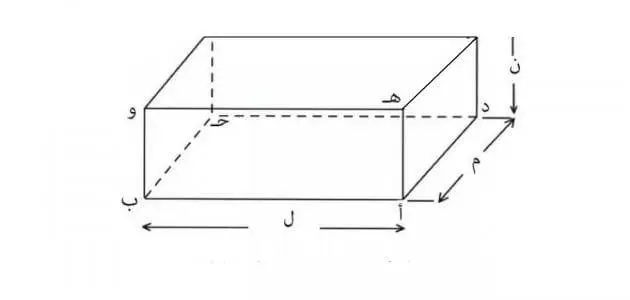
تعريف متوازي المستطيلات
- يمكن تعريف متوازي المستطيلات على أنه كيان ثلاثي الأبعاد، أي أن لها الطول والعرض والارتفاع، والشكل مشابه لشكل الصندوق، وعادة ما يعتبر حالة خاصة للمنشور، ويتكون من الأجزاء التالية:
- الوجه: المنشور المستطيل له ستة أوجه مستطيلة تسمى الوجوه المستطيلة.
- الأحرف: (بالإنجليزية: edges) هي الحواف التي تشكل سطحًا، والتي يمكن تعريفها بطريقة أخرى كخط مستقيم يربط بين رأسين متجاورين في شكل متوازي المستطيلات.
- الرأس: هذه هي النقطة أو الزاوية التي تلتقي فيها الأحرف الثلاثة بخط متوازي السطوح، وتكون جميعها في وضع مستقيم.
شاهد أيضًا: مساحة متوازي المستطيلات ومحيطه
خصائص متوازي المستطيلات
- بالإضافة إلى تلك المذكورة في التعريف السابق، تتميز المناشير المستطيلة أيضًا بمجموعة من الخصائص وهي:
- كل زوج من الوجوه المتقابلة في منشور الزاوية اليمنى متوازي ومتسق تمامًا.
- لمنشور الزاوية القائمة ستة أوجه وثمانية رؤوس واثنا عشر حرفًا.
- الحواف المعاكسة للمنشور متوازية.
- وتجدر الإشارة هنا إلى أنه إذا تساوى الطول والعرض والارتفاع، فإن المكعب يسمى المكعب.
حجم متوازي المستطيلات
يمكن حساب حجم متوازي المستطيلات ثلاثي الأبعاد بالصيغة التالية:
- حجم متوازي المستطيلات= الطول×العرض×الارتفاع
- وفي الرمز: H = A × B × C
- H: حجم متوازي المستطيلات.
- A: طول متوازي المستطيلات.
- B: عرض متوازي المستطيلات.
- C: ارتفاع متوازي المستطيلات.
أمثلة على حساب حجم متوازي المستطيلات
1- المثال الأول
- ما هو حجم المنشور المستطيل بطول 14 سم وعرض 12 سم وارتفاع 8 سم؟
- الحل: حجم متوازي المستطيلات = الطول × العرض × الارتفاع.
- لذا: حجم متوازي المستطيلات = 14 × 12 × 8 = 1344 سم3
2- المثال الثاني
- ما هو حجم خط متوازي طوله 14 سم وعرضه 50 مم وارتفاعه 10 سم؟
- الحل: حجم متوازي المستطيلات = الطول × العرض × الارتفاع
- نظرًا لأن الطول والارتفاع بالسنتيمتر، يجب تحويل العرض إلى سنتيمترات بحيث تكون جميع الأبعاد في نفس الوحدة، ومن المعروف أن 10 مم = 1 سم فيكون العرض يساوي: 50 مم / 10 سم = 5 سم.
- نظرًا لأن الأبعاد في نفس الوحدة، يمكن إيجاد الحجم التالي: حجم المنشور المستطيل = 14 × 5 × 10 = 700 سم 3.
3- المثال الثالث
- عند شراء جدار متوازي مستطيل الشكل بارتفاع 7.5 سم وطول 25 سم وعرض 10 سم يكون كل 1000 طوبة بطول 20 مم وارتفاع 2 مم وعرض 0.75 مم ما هي تكلفة؟ تساوي 900 قطعة نقدية؟
- الحل: يمثل حجم الجدار حجم متوازي المستطيلات، والذي يمكن حسابه على النحو التالي:
- حجم الجدار = الطول × العرض × الارتفاع = 20 م × 2 م × 0.75 م = 30 م³.
- يمثل حجم الطوب أيضًا حجم متوازي المستطيلات، والذي يمكن حسابه على النحو التالي قالب القرميد = 25 سم × 10 سم × 7.5 سم = 1875 سم مكعب.
- عدد الطوب المطلوب = حجم الجدار / حجم الطوب ماعدا أن حجم الطوب بالسنتيمتر المكعب وحجم الجدار بالمتر المكعب لذلك يجب تحويل حجم الجدار بقسمة الحجم على القيمة (1،000،000) سنتيمتر مكعب لتوحيد الوحدة.
- لأن كل 1m³ = 1،000،000cm³، حيث: حجم الطوب (متر مكعب) = 1875 / 1000000 = 0.001875 م.
- عدد الطوب = 30 / 0.001875 = 16000 طوبة.
- العملية التناسبية، النسبة بين كمية القالب وتكلفته هي كما يلي:
- كل 1000 مربع ← 900 قطعة نقدية
- لكل 16000 مربع ←؟؟
- بإجراء الضرب التبادلي، تكون تكلفة الكتلة = 900 × 16000/1000، أي ما يعادل 14400 قطعة نقدية.
4- المثال الرابع
- يبلغ طول المسبح الأولمبي 50 مترا وعرضه 25 مترا وعمقه مترين ما هي كمية المياه التي يمكن أن يتسع لها المسبح؟
- الحل: يمكن التعبير عن كمية الماء في البركة بالحجم، وحجم الماء يساوي حجم متوازي المستطيلات، ويمكن أن يكون على النحو التالي:
- حجم متوازي المستطيلات =
- الطول × العرض × الارتفاع = 50 × 25 × 2 = 2500 متر مكعب، وهي كمية الماء في البركة.
5- المثال الخامس
- إذا كان طول متوازي المستطيلات 8 سم وارتفاعه 3 سم، فما عرضه إذا كان حجمه 120 سم 3؟
- الحل: حجم متوازي المستطيلات = الطول × العرض × الارتفاع.
- ومن ثم، 120 = 8 × العرض × 3. بحل هذه المعادلة، يكون العرض = 5 سم.
6- المثال السادس
- صمم فؤاد صندوقًا على شكل مستطيل متوازي السطوح بحجم 2500 سم 3 وارتفاع 25 سم وقاع مربع، ثم أدرك أنه بحاجة إلى صندوق أصغر، فقصه من ارتفاعه إلى 1000 سم بحجم 3.
- تظل المساحة الموجودة في الأسفل كما هي، وبالتالي يصبح الارتفاع مرتفعًا جدًا، ويصبح شكل الصندوق مكعبًا؟
- الحل: استخدم صيغة حجم متوازي المستطيلات = الطول × العرض × الارتفاع لحساب المساحة السفلية.
- بما أن الحجم = 2500 سم 3 والارتفاع = 25 سم، واستبدال هذه القيم بقانون الحجم، يمكنك الحصول على مساحة القاعدة المربعة على النحو التالي:
- 2500 = (الطول × العرض) × الارتفاع = (الطول × العرض) × 25، بقسمة كلا الجانبين على (25)، يمكنك أن ترى بوضوح: 100 سم 2 = الطول × العرض، والتي تمثل مساحة القاعدة.
- احسب طول وعرض المربع الأساسي كما يلي:
- المساحة الأساسية = (طول الضلع) 2، بدءًا منه: طول الضلع = 100√ = 10 سم، وبما أن الأساس مربع، فإن عرضه أيضًا يساوي 10 سم.
- باستخدام قانون الحجم في خط متوازي السطوح المستطيل، بعد قطع جزء من الارتفاع، احسب ارتفاع الصندوق، واحصل على: حجم الصندوق بعد القطع = الطول × العرض × الارتفاع، ومنه:
- 1000 = 10 × 10 × ارتفاع نتيجة قسمة كلا الجانبين على (100) هي: ارتفاع جديد = 10 سم.
- بما أن الطول = العرض = الارتفاع، فإن الشكل الناتج يكون مكعبًا.
7- المثال السابع
- ما مقدار الهواء في الغرفة على شكل مستطيل متوازي السطوح بطول 5 أمتار وعرض 6 أمتار وارتفاع 10 أمتار؟
- الحل: كمية الهواء في الغرفة = سعة الغرفة = حجم المستطيل.
- حجم متوازي المستطيلات = الطول × العرض × الارتفاع، حجم متوازي المستطيلات = 5 × 6 × 10 = 300 متر مكعب، فيكون حجم الهواء في الغرفة 300 متر مكعب.
8- المثال الثامن
- قضيب معدني على شكل متوازي المستطيلات طوله 10 أمتار وعرضه 60 سم وسمكه 25 سم وإذا كان المتر المكعب يكلف 250 دولار فما هو سعره؟
- الحل: لحساب سعر العمود المعدني، يجب عليك أولاً حساب حجمه، لأن السعر = التكلفة لكل متر مكعب × حجم المنشور المستطيل، يمكنك الحصول على:
- حجم متوازي المستطيلات = الطول × العرض × الارتفاع = 10 × (60/100) × (25/10)، وتجدر الإشارة إلى أنه تم تقسيمه على 100 لتحويل سم إلى متر.
- حجم منشور الزاوية اليمنى = 1.5 متر مكعب، سعر العارضة المعدنية = 1.5 × 250 = 375 دولار أمريكي.
9- المثال التاسع
- ما هو ارتفاع متوازي المستطيلات بافتراض أن حجمه 300 سم 3 ومساحته السفلية 30 سم؟
- الحل: حجم متوازي المستطيلات = الطول × العرض × الارتفاع، ويمكن إيجاد الارتفاع على النحو التالي:
- القاع مستطيل، لذا مساحته = الطول × العرض، وهو ما يساوي 30 سم.
- يمكن إيجاد الارتفاع من معادلة الحجم على النحو التالي: 300 = 30 × الارتفاع، منه الارتفاع: 300/30 = 10 سم.
شاهد أيضًا: شكل متوازي المستطيلات في الرياضيات
10- المثال العاشر
- حوض سباحة فارغ على شكل خط متوازي مستطيل طوله 25 مترًا وعرضه 10 مترًا وعمقه 2 مترًا ويمكن ملئه بالماء بمعدل 800 لتر في الدقيقة.
- لذلك من المعروف تمامًا عدد الدقائق وعدد الدقائق التي يستغرقها المتر المكعب = 1000 لتر ساعات لملئه؟
- الحل: لحساب كمية الماء المطلوبة لملء البركة، يمكنك استخدام قانون حجم متوازي المستطيلات = الطول × العرض × الارتفاع لحساب، ثم الحصول على:
- حجم متوازي المستطيلات = 25 × 10 × 2 = 500 م3 وهي كمية الماء اللازمة لملء البركة.
- الوقت اللازم للتعبئة الكاملة = الحجم / معدل التعبئة، والفرق هو أن معدل التعبئة يجب أن يقسم أولاً على لتر على (1000)، ثم تحويله من لتر إلى متر مكعب.
- لأن كل متر مكعب = 1000 لتر أي 800 لتر / دقيقة = 800/1000 = 0.8 م / دقيقة، لذلك:
- الوقت المطلوب لملء المسبح بالكامل = 500 م / ((0.8) م³ / دقيقة) حيث الوقت بالدقائق = 625 دقيقة والوقت بالساعات = 625/60 = حوالي 10 ساعات ونصف.
11- المثال الحادي عشر
- إذا كان حجم قاع الصندوق أ (أي الطول والعرض) هو: 10 سم × 8 سم، وكان حجم قاع المربع ب: 15 سم × 10 سم، يكون الصندوقان أ وب على شكل متوازي سطوح مستطيل.
- صب الماء في الصندوق (ب) ما ارتفاع الماء في الصندوق؟
- الحل: كمية الماء (الحجم) في المربع أ = كمية الماء (الحجم) في المربع ب، ثم استبدل قانون حجم المستطيل شبه المكعب = الطول × العرض × الارتفاع.
- ثم تصبح: 10 × 8 × 15 = 15 × 10 × ارتفاع، ويتم الحصول عليها عن طريق حل المعادلة: الارتفاع = 8 سم.
12- المثال الثاني عشر
- إذا كان حجم الصندوق المستطيل 1440 م 3 وطوله 15 م وارتفاعه 8 م فما ارتفاعه؟
- الحل هو: حجم متوازي المستطيلات = الطول × العرض × الارتفاع.
- ونحصل منه على: 1440 = 15 × 8 × الارتفاع، وبحل المعادلة يكون واضحًا.
- الارتفاع = 1440/120 = 12 م.
13- المثال الثالث عشر
- إذا كان حجم قاع صندوق مستطيل 80 سم × 40 سم، وكان الحجم 160 لترًا.
- فإن أحمد يريد أن يرسم من جميع الجوانب ما عدا قاع الصندوق، وتبلغ تكلفة الطلاء 6000 قطعة نقود / مربع، يرجى معرفة تكلفة الرسم؟
- الحل: استخدم صيغة الحجم لمنشور مستطيل لحساب ارتفاع الصندوق، باستثناء أنه يجب عليك أولاً تحويل لتر واحد إلى سنتيمترات مكعبة لمضاعفة الحجم في (1000) لتوحيد الوحدة.
- لأن 1 لتر = 1000 سم مكعب، تحصل على: حجم المنشور المستطيل = 160 لترًا = 160.000 سم مكعب.
- ثم استبدل هذه القيمة في صيغة حجم متوازي المستطيلات: الطول × العرض × الارتفاع، وستحصل على:
- 000 = 80 × 40 × ارتفاع، بدءًا من هذا الارتفاع: الارتفاع = 50 سم.
- مساحة المنشور المستطيل، باستثناء الجزء السفلي = المنطقة الجانبية + منطقة القاع العليا =
- 2 × الارتفاع × (الطول + العرض) + الطول × العرض =
- 2 × 50 × (80 + 40) + 80 × 40 = 15200 سم² = 1.52 م²، لأن كل 1 م² = 1000 سم².
- حساب تكلفة الطلاء = مساحة الصندوق × تكلفة الطلاء = 1.52 متر مربع × 6000 قطعة نقدية / متر مربع = 9،120 قطعة نقدية.
شاهد أيضًا: متوازي المستطيلات والمكعب
لقد ناقشنا في مقالة اليوم قانون حجم متوازي المستطيلات، كما وضحنا الأمثلة المفصلة على القانون لمساعدة الطلبة على حل جميع المسائل المتعلقة بهذا الموضوع.