متوازي المستطيلات والمكعب
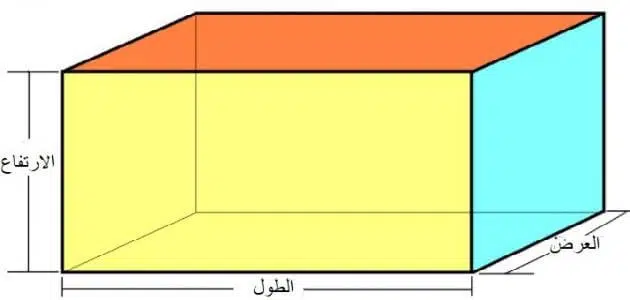
متوازي المستطيلات والمكعب، يعتبر متوازي المستطيلات من أهم الأشكال الهندسية الموجودة في الطبيعة، وقد نراه في الحالات المختلفة في حياتنا اليومية، بالإضافة إلى المكعب الذي لا يقل أهمية عن متوازي المستطيلات.
تعريف متوازي المستطيلات
- متوازي المستطيلات هو أحد الأشكال الهندسية أو المجسمات ثلاثية الأبعاد.
- متوازي المستطيلات له طول وعرض وارتفاع.
- يشبه متوازي المستطيلات في شكله الصندوق، ويتم اعتباره شبيهًا بالمنشور ولكنه حالة خاصة منه.
شاهد أيضًا: موضوع عن قانون حجم المكعب
مكونات متوازي المستطيلات
- يتكون متوازي المستطيلات من ستة أوجه، وتكون تلك الأوجه على شكل مستطيلات، وتسمى بأوجه متوازي المستطيلات.
- الحواف الموجودة على أسطح متوازي المستطيلات تسمى الأحرف أو الحروف، ويتم تعريفها في علم الرياضيات بأنها الخطوط المستقيمة التي تصل بين كل رأسين متجاورين في متوازي المستطيلات.
- الزوايا أو النقاط التي تتقابل عندها ثلاثة أحرف من متوازي المستطيلات تسمى الرؤوس، وجميعها تكون زوايا قائمة.
خصائص متوازي المستطيلات
- في متوازي المستطيلات، كل زوج من الوجوه المتقابلة تكون متطابقة تمامًا، ومتوازية.
- متوازي المستطيلات له ستة أوجه، واثنا عشر حرفًا، وثمانية رؤوس.
- في متوازي المستطيلات، الحواف المتقابلة تكون دائمًا متوازية.
- عند تساوي الطول والعرض والارتفاع لمتوازي المستطيلات، فإنه يسمى مكعب في هذه الحالة.
مساحة متوازي المستطيلات
- المساحة الكلية لمتوازي المستطيلات تساوي ضعف ضرب الطول × العرض × الارتفاع، أو يتم الرمز إليها في علم الرياضيات كالآتي: م = 2 × (س × ص + س × ع + ص × ع).
- يرمز الرمز (س) إلى طول متوازي المستطيلات.
- الرمز (ص) هو عرض متوازي المستطيلات.
- الرمز (ع) هو ارتفاع متوازي المستطيلات.
- وتمثل (م) مساحة متوازي المستطيلات.
المساحة الجانبية لمتوازي المستطيلات
- المساحة الجانبية لمتوازي المستطيلات هي مجموع مساحة جميع الأوجه ما عدا القاعدتين.
- أو بطريقة أخرى 2 × (الطول + العرض) × الارتفاع.
- وفي علم الرياضيات يتم الرمز للمساحة الجانبية لمتوازي المستطيلات بـ 2 × (س + ص) × ع.
- أو يمكننا القول إن المساحة الجانبية لمتوازي المستطيلات تساوي المساحة الجانبية + مساحة القاعدتين.
شرح مساحات متوازي المستطيلات
- متوازي المستطيلات متعدد الأوجه وهما ستة أوجه.
- لإيجاد مساحة متوازي المستطيلات، يجب إيجاد مساحة جميع الأوجه الموجودة في متوازي المستطيلات المراد إيجاد مساحته.
- ويمكن إيضاح ذلك بأن مساحة متوازي المستطيلات تساوي مساحة الوجه الأول + مساحة الوجه الثاني + مساحة الوجه الثالث + مساحة الوجه الرابع + مساحة الوجه الخامس + مساحة الوجه السادس.
- من المعروف أن جميع أوجه متوازي المستطيلات متساوية في المساحة، فإن المساحة تساوي 2 × مساحة الوجه الأول أو مساحة القاعدتين + 2 × مساحة الوجه الثاني أي أول وجهين جانبيين.
- ويمكن القول بطريقة أخرى، 2 × الطول × العرض (وهما مساحة القاعدتين) + 2 × العرض × الارتفاع (وهي مساحة الوجهين الجانبيين الآخرين).
- مع العلم أن مساحة المستطيل تساوي حاصل ضرب الطول في العرض.
أمثلة لحساب مساحة متوازي المستطيلات
- متوازي مستطيلات طول قاعدته 10 متر، وعرضه 4 متر، وارتفاعه يساوي 5 متر، قم بحساب مساحة متوازي المستطيلات الكلية.
- لحساب مساحة متوازي المستطيلات في المثال السابق يتم استخدام قانون المساحة الكلية، وهو 2 × (الطول × العرض + الطول × الارتفاع + العرض × الارتفاع)، فتكون مساحة متوازي المستطيلات تساوي 220 متر مربع.
- صندوق على شكل متوازي مستطيلات، طول قاعدته يساوي 40 سم، وعرضها يساوي 31 سم، وارتفاعها يساوي 12 سم، احسب المساحة الكلية لتغليف الصندوق بالكامل بورق الهدايا.
- مساحة ورق الهدايا الذي نحتاجه لتغليف الصندوق في المثال السابق تساوي 2 × (الطول × العرض + الطول × الارتفاع + العرض × الارتفاع) ويساوي 4.18 متر مربع.
حجم متوازي المستطيلات
- يتمثل حكم متوازي المستطيلات في مقدار الفراغ الموجود داخل المتوازي، ويتم حسابها عن طريق حاصل ضرب الطول × العرض × الارتفاع لمتوازي المستطيلات المراد حساب حجمه.
- وفي العلاقة الرياضية تكون بالشكل: (م = س × ص × ع).
- يرمز الرمز (س) إلى طول متوازي المستطيلات.
- الرمز (ص) هو عرض متوازي المستطيلات.
- الرمز (ع) هو ارتفاع متوازي المستطيلات.
- وتمثل (م) مساحة متوازي المستطيلات.
مثال على حساب حجم متوازي المستطيلات
- كشكول صغير على شكل متوازي المستطيلات، يبلغ طول قاعدته 6 سم، وعرضها 4 سم، ويبلغ ارتفاعه 1 سم، احسب حجم الصفحات اللازمة لملء الكشكول.
- يتم حساب حجم الكشكول في المثال السابق لمعرفة حجم الصفحات، عن طريق إيجاد حاصل ضرب الطول × العرض × الارتفاع وهو يساوي 24 سم مكعب.
- أي أن الكشكول يحتاج 24 سم مكعب من الورق لتعبئته.
المكعب
- حسب الهندسة الإقليدية، يتم تعريف المكعب على أنه مجسم صلب يتكون من أوجه منتظمة الشكل.
- يتكون المكعب من ستة أوجه، كل وجه عبارة عن مربع، وتطابق جميع الأوجه مع بعضها، حتى تشكل القمم والحواف للمكعب.
- يُطلق على المكعب أيضًا اسم “سداسي الأوجه”.
- يعتبر المكعب من المجسمات الخمسة التي يطلق عليها المواد الصلبة الأفلاطونية.
- يطلق مصطلح المواد الصلبة الأفلاطونية على المجسمات التي تكون كل أوجهها مضلعة ومتماثلة ومنتظمة.
1- أجزاء المكعب
- يتكون المكعب من خمسة أجزاء مختلفة، الجزء الأول هو الوجه أو الجانب، حيث يتكون المكعب من 6 أوجه متساوية في الحجم ومتشابهة في الشكل، ولكل وجه أربع زوايا قائمة.
- الجزء الثاني هو عدد 12 حافة، أو ضلع، جميعهم متساويين في الطول، والحافة هي خط التقاء الرأسين معًا في المكعب.
- المكعب له عدد 8 رؤوس، والرأس عبارة عن نقطة التقاء ثلاثة حواف معًا في جسم المكعب.
- يتكون المكعب من 12 قطرًا ثنائي الأبعاد، والخط الثنائي الأبعاد هو الخط الذي يصل بين الرؤوس المتعاكسة في كل وجه.
- القطر الآخر هو قطر ثلاثي الأبعاد، ويتكون المكعب من عدد 4 أقطار داخلية ثلاثية الأبعاد، والخط الثلاثي الأبعاد هو الخط الذي يربط بين الزوايا المتعاكسة للمكعب من الداخل.
2- خصائص المكعب
- كل وجه من أوجه المكعب مرتبط مع أربعة أوجه أخرى من نفس المكعب.
- جميع زوايا المكعب هي زوايا قائمة، أي أنها تساوي 90 درجة.
- يتكون رأس المكعب من التقاء ثلاثة أضلع من أضلاعه معًا.
- كل الحواف المتقابلة تتوازى مع بعضها في نفس الوجه في المكعب.
شاهد أيضًا: شكل متوازي المستطيلات في الرياضيات
3- مساحة المكعب
- يتكون المكعب من ستة أوجه مربعة الشكل، لذلك، يجب معرفة كيفية حساب مساحة المربع للتوصل إلى حساب مساحة المكعب.
- يعتبر المربع شكل هندسي شبيه بالمستطيل، حيث أنه حالة خاصة منه، إلا أن المربع أطوال أضلاعه متساوية، أما المستطيل فله طول وله عرض مختلفين عن بعضهما في القياس.
- يتم حساب مساحة المستطيل عن طريق إيجاد حاصل ضرب الطول × العرض.
- بما أن المربع طوله متساوٍ مع عرضه، إذًا يمكننا الحصول على مساحة المربع عن طريق ضرب طول ضلعه في نفسه.
- ويكون قانون حساب مساحة المربع في علم الرياضيات كالآتي (م = س × س) أو (م = س2).
- حيث أن (م) تمثل مساحة المربع.
- (س) تمثل طول ضلع المربع.
- وبالتالي يتم حساب مساحة المكعب عن طريق حساب مجموع مساحات أوجه المكعب.
4- مساحة المكعب الكلية
- بما أن جميع أوجه المكعب متماثلة تمامًا في الشكل والمساحة، فيمكن حساب مساحة أحد مربعات المكعب وضربها في عدد أوجه المكعب وهو 6 أوجه.
- وبالتالي تكون المساحة الكلية للمكعب = س2 × 6.
- حيث أن (س) تساوي طول ضلع وجه المكعب.
5- مساحة السطح الجانبي للمكعب
- هي مجموع مساحات أوجه المكعب ما عدا الوجه العلوي والوجه السفلي.
- وبالتالي يمكن حساب مساحة السطح الجانبي للمكعب عن طريق القانون 4 × س2، حيث (س) تساوي طول ضلع أحد أوجه المربع.
أمثلة على حساب مساحة المكعب
- مكعب طول ضلع أحد أوجهه 3 سم، قم بحساب مساحة هذا المكعب.
- نقوم بالتعويض في القانون م = 6 × س2، وبالتالي مساحة المكعب = 6 × 3 أس 2 تساوي 54 سم مربع.
- احسب المساحة الكلية لمكعب طول ضلع أحد أوجهه يساوي 7 سم.
- في المثال السابق، نقوم بحساب مساحة المكعب عن طريق حساب مساحة وجه المكعب وهو 7 × 7 = 49، ونقوم بضرب مساحة وجه المكعب في 6 وهو عدد أوجه المكعب، أي أن مساحة المكعب السابق تساوي 294 سم مكعب.
6- حساب مساحة المكعب من حجمه
- في البداية، يتم حساب طول ضلع المكعب من خلال قانون حجم المكعب، ويمكن حسابه باستخدام الآلة الحاسبة، أو عن طريق إيجاد الرقم الذي يتم ضربه في نفسه ثلاث مرات ويعطيك حجم المكعب الموجود أمامك.
- بعد حساب طول ضلع المكعب، يتم حساب قانون مساحة المكعب، وسنذكر لك مثالًا لتوضيح طريقة الحساب.
- إذا كان لديك مكعب حجمه 125 سم مكعب، فكيف يمكنك حساب مساحته؟
- يمكنك إيجاد مساحة المكعب عن طريق حساب الجذر التكعيبي لحجم المكعب، أي الجذر التكعيبي لـ 125 وهو 5.
- إذًا، طول ضلع وجه المكعب المطلوب حساب مساحته هو 5 سم.
- وبالتالي يمكن معرفة مساحة المكعب عن طريق القانون 6 × 5 أس 2، أي أن مساحة المكعب تساوي 150 سم مربع.
شاهد أيضًا: مساحة متوازي المستطيلات ومحيطه
وضحنا ما هو متوازي المستطيلات، وما هي أهم خصائصه، وكيف يمكننا حساب حجمه ومساحته وذكر الأمثلة على ذلك، وعرفنا ما هو المكعب وما هي خصائصه وكيف نحسب مساحته وحجمه.