مساحة متوازي المستطيلات ومحيطه
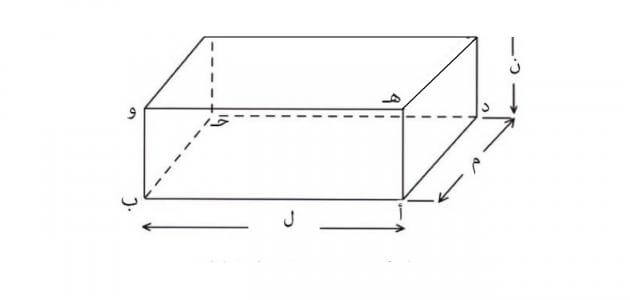
مساحة متوازي المستطيلات ومحيطه، يتكون متوازي المستطيلات من ستة أوجه، ويمكن من خلال إيجاد مجموع مساحات هذه الأوجه حساب مساحته، إن الأوجه المتقابلة في متوازي المستطيلات تكون متطابقة لذلك عند إيجاد مساحته نحتاج إلى ثلاثة أوجه فقط.
تعريف متوازي المستطيلات
- متوازي المستطيلات هو أحد المجسمات التي لها أبعاد ثلاثية، بمعني أن لمتوازي المستطيلات طول وعرض وارتفاع، ويمكن تشبيهه بشكل الصندوق، وبشكل عام فهو حالة خاصة من المنشور.
- يتكون متوازي المستطيلات من وجوه، وأحرف، ورؤوس، فلمتوازي المستطيلات ستة أسطح على شكل مستطيلات تعرف باسم الوجوه.
- هذه الوجوه التي يتكون منها متوازي المستطيلات لها حواف ويمكن أن نطلق عليها أنها خطوط مستقيمة تصل بين كل رأسيين متجاورين في متوازي المستطيلات.
- عند تلاقي ثلاثة أحرف من متوازي المستطيلات تتكون نقاط أو زوايا تُعرف بالرؤوس وجميعها قائمة.
خصائص متوازي المستطيلات
- يمتاز متوازي المستطيلات بأن كل وجهين متقابلين في متوازي المستطيلات متوازيين ومتطابقين تماما، وأن متوازي المستطيلات يحتوي على ستة أوجه.
- يحتوي متوازي المستطيلات على ثمانية رؤوس، واثنا عشر حرفاً، ويتميز متوازي المستطيلات بأن الحروف المتقابلة فيه متوازية.
- هناك حالة خاصة لمتوازي المستطيلات وهي أنه إذا تساوى الطول، والعرض، والارتفاع في الطول فيُعرف وقتها متوازي المستطيلات باسم المكعب.
قانون مساحة متوازي المستطيلات
- يمكننا حساب مساحة متوازي المستطيلات باستخدام قانون المساحة الكلية لمتوازي المستطيلات =2× (س× ص+ س× ع +ص ×ع) حيث أن س رمز يعبر عن طول متوازي المستطيلات، وص يعبر عن عرضه، وع ارتفاعه.
- يمكننا حساب المساحة الجانبية لمتوازي المستطيلات، أي حساب مجموع مساحة أوجه متوازي المستطيلات عدا القاعدتين من خلال قانون المساحة الجانبية= 2× (الطول + العرض) ×الارتفاع.
- يمكننا القول بأن المساحة الكلية لمتوازي المستطيلات = المساحة الجانبية له + مساحة القاعدتين لمتوازي المستطيلات.
تفاصيل عن مساحات متوازي المستطيلات
- نعرف أن متوازي المستطيلات هو من الأشكال الهندسية التي لها أوجه متعددة، ولكي نتمكن من إيجاد مساحة متوازي المستطيلات يجي علينا إيجاد مساحات الأوجه الستة الذي يحتوي عليهم.
- بشكل أبسط يمكن أن نقول إن مساحة متوازي المستطيلات= مساحة الوجه الأول+ مساحة الوجه الثاني+ مساحة الوجه الثالث + مساحة الوجه الرابع+ مساحة الوجه الخامس+ مساحة الوجه السادس.
- لقد ذكرنا أيضاً أن كل وجهين متقابلين من أوجه متوازي المستطيلات متوازيين ومتطابقين فيمكننا إيجاد المساحة بشكل آخر.
- مساحة متوازي المستطيلات=2 × مساحة الوجه الأول + 2× مساحة الوجه الثاني + 2 × مساحة الوجه الثالث+ 2 × الطول × العرض +2×العرض× الارتفاع + 2 × الطول × الارتفاع ونعلم أن مساحة المستطيل =الطول× العرض.
- بشكل آخر مساحة متوازي المستطيلات= مساحة القاعدتين+ مساحة أول وجهين جانبيين+ مساحة القاعدتين+ مساحة أول وجهين جانبيين+ مساحة ثاني وجهين جانبيين.
أمثلة على حساب مساحة متوازي المستطيلات
1- المثال الأول
متوازي مستطيلات، طول قاعدته 5 م، وعرض قاعدته 2م، وارتفاعه يساوي 2ونص م. فما هي المساحة الجانبية لمتوازي المستطيلات.
الحل
- سنستخدم قانون المساحة الكلية لمتوازي المستطيلات=2× (الطول× العرض +الطول × الارتفاع +الارتفاع ×العرض).
- أي أن المساحة الكلية لمتوازي المستطيلات=2× (5×2+5×2.5+2×2.5) =110م مربع.
2- مثال ثاني
صندوق على شكل متوازي مستطيلات طول قاعدته 40 سم، وعرض القاعدة 31سم، وارتفاعه 12 سم فما هي مساحته الكلية.
الحل
- سنستخدم قانون المساحة الكلية لمتوازي المستطيلات=2× (الطول ×العرض +الطول × الارتفاع +الارتفاع ×العرض).
- أي أن المساحة الكلية لمتوازي المستطيلات=2× (40×31+40×12+31×12) =4.184 متر مربع.
3- مثال آخر
متوازي مستطيلات طول قاعدته 3سم، وعرضه قاعدته 5سم، وارتفاعه يساوي4 سم فما هي مساحته الجانبية.
الحل
- سنستخدم قانون المساحة الجانبية لمتوازي المستطيلات= 2× (الطول +العرض) × الارتفاع.
- أي أن المساحة الجانبية لمتوازي المستطيلات = 2× (3+5) ×4.
حجم متوازي المستطيلات
حجم متوازي المستطيلات يعير عن كمية المقدار الفارغ الموجود بداخله ويمكننا حساب حجم متوازي المستطيلات باستخدام قانون حجم متوازي المستطيلات = الطول × العرض× الارتفاع.
أمثلة على حجم متوازي المستطيلات
1- المثال الأول
متوازي مستطيلات طول قاعدته 3 سم، وعرض قاعدته 2سم، وارتفاعه يساوي نص سم فما هو حجم متوازي المستطيلات.
الحل
- سنقوم باستخدام قانون حجم متوازي المستطيلات حيث أن حجم متوازي المستطيلات = الطول × العرض × الارتفاع.
- أي أن حجم متوازي المستطيلات= 3×2×0.5=12 سم مكعب.
2- مثال آخر
متوازي مستطيلات طول قاعدته 12 سم، وعرض قاعدته 5 سم، وارتفاعه يساوي 2.4 سم فما هو حجم متوازي المستطيلات.
الحل
- سنقوم باستخدام قانون حجم متوازي المستطيلات حيث أن حجم متوازي المستطيلات = الطول × العرض × الارتفاع.
- أي أن حجم متوازي المستطيلات= 12×5×2.4= 144سم مكعب.
أقطار متوازي المستطيلات
- يحتوي متوازي المستطيلات على نوعين مختلفين من الأقطار وهما أقطار الوجه، وأقطار متوازي المستطيلات.
- أقطار الوجه، هي التي تربط وتوصل بين كل زاويتين متقابلتين لأوجه متوازي المستطيلات وهي خطوط مستقيمة، ويحتوي متوازي المستطيلات على اثني عشر قطراً حيث أن لكل وجه من أوجه المتوازي قطران.
- يمكننا حساب طول أقطار الوجه من خلال قانون طول قطر القاعدتين = الجذر التربيعي ل (مربع الطول + مربع العرض)، وطول قطر أول وجهين = الجذر التربيعي ل (مربع الطول + مربع الارتفاع).
- ويمكننا حساب طول قطر ثاني وجهيين جانبيين من خلال قانون طول قطر ثاني وجهيين جانبيين = الجذر التربيعي ل (مربع العرض+ مربع الارتفاع).
أمثلة متنوعة على متوازي المستطيلات
1- المثال الأول
متوازي مستطيلات حجمه يساوي 792 متر مكعب، ومساحة قاعدته تساوي 132 متر مربع فما هو ارتفاع متوازي المستطيلات.
الحل
- سنستخدم قانون حجم متوازي المستطيلات= الطول× العرض× الارتفاع، وبما أن مساحة القاعدة = 132 اذاً الطول × العرض= 132 متر مربع.
- عند تطبيق ذلك في قانون حجم متوازي المستطيلات اذاً الارتفاع= 792 ÷ 132= 6 متر.
2- مثال آخر
متوازي مستطيلات ارتفاعه يساوي 3 سم، وعرض قاعدته يساوي 4 سم، وطول قاعدته يساوي 5 سم فما هو حجمه وما هي مساحته الكلية.
الحل
- سنستخدم قانون حجم متوازي المستطيلات = الطول × العرض× الارتفاع، اذاً حجم متوازي المستطيلات = 5×4× 3= 60 سم مكعب.
- سنستخدم قانون المساحة الكلية لمتوازي المستطيلات=2× (الطول× العرض +الطول × الارتفاع +الارتفاع ×العرض).
3- مثال آخر
متوازي مستطيلات طوله 8 سم، وعرضه يساوي 6 سم، وحجمه يساوي 192 سم مكعب فما هو ارتفاعه ومساحته الجانبية ومساحته الكلية.
الحل
- سنستخدم قانون حجم متوازي المستطيلات حيث أن حجم متوازي المستطيلات = الطول × العرض× الارتفاع ومنه سنجد أن الارتفاع يساوي 4 سم.
- سنستخدم قانون المساحة الكلية لمتوازي المستطيلات=2× (الطول× العرض +الطول × الارتفاع+ الارتفاع ×العرض)، ومنه فإن المساحة الجانبية لمتوازي المستطيلات تساوي 208 سم مربع.
- وسنستخدم قانون المساحة الجانبية لمتوازي المستطيلات حيث أن المساحة الجانبية لمتوازي المستطيلات= 2× (الطول+ العرض) × الارتفاع.
محيط متوازي المستطيلات
- محيط متوازي المستطيلات هو الخيط الذي يلتف حول الشكل الذي يكون ثنائي الأبعاد من هذه الأشكال المربع والمستطيل، والدائرة، والمثلث، لمتوازي الأضلاع.
- فبذلك لا يمكن أبداً حساب محيط متوازي المستطيلات ولكن يمكن الاستعاضة عنه بحساب المساحة الجانبية لمتوازي المستطيلات كما ذكرنا.
- ومحيط أي مضلع هو مجموع أضلاعه الخارجية وبالتالي فمحيط متوازي المستطيلات هو مساحة أوجه متوازي المستطيلات.
لقد ذكرنا في مقال مساحة متوازي المستطيلات ومحيطه، تعريف متوازي المستطيلات، وخصائصه، ومساحته الجانبية التي تعتبر هي محيط متوازي المستطيلات، وحجمه، وجميع القوانين التي تساعدنا على حل جميع مسائل متوازي المستطيلات.