مساحة المثلث متساوي الأضلاع والقائم
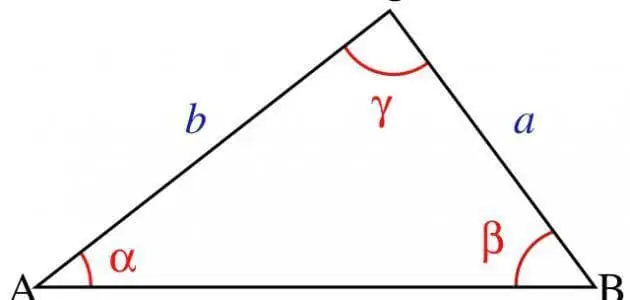
مساحة المثلث متساوي الأضلاع والقائم، في المثلث متساوي الأضلاع القائم الزاوية، تتطابق جميع الاضلاع لجوانب المثلث الثلاثة، بينما لا تطابق زوايا المثلث، لأن مجموع زوايا المثلث يساوي 180 درجة، وحيث انه مثلث قائم الزاوية فإن إحدى زواياه تساوي 90 درجة، والزاويتين الأخريين مجموعهم أيضًا 90 درجة، في هذا المقال سوف نشرح كيفية استنتاج مساحة المثلث متساوي الأضلاع والقائم.
نظرة عامة حول المثلث القائم متساوي الأضلاع
- يتم تعريف المثلث متساوي الأضلاع قائم الزاوية بأنه مجسم منتظم يتكون من ثلاثة أضلاع، منهم ضلعين متساويين في الطول.
- تحصر الأضلاع الثلاثة للمثلث ثلاثة زوايا، مكونة ثلاثة رؤوس للمثلث.
- من البديهيات أن يكون مجموع طول ضلعين في المثلث أكبر من طول الضلع الثالث.
- مجموع زوايا المثلث الثلاثة يساوي 180 درجة.
- المثلث القائم هو الذي يكون قياس إحدى زواياه تساوي 90 درجة، مجموع قياس الزاويتين الآخرين يساوي 90 درجة ايضًا.
- ساقي المثلث هما الضلعان حيث يحصران الزاوية التي تساوي 90 درجة (الزاوية القائمة) بينهما، ويطلق عليهما ضلعي القائمة.
- الوتر هو الضلع الذي يقابل الزاوية القائمة، ويكون هو الضلع الاطول طولًا في المثلث قائم الزاوية.
شاهد أيضًا: اشكال مطويات رياضيات جاهزة للطباعة
مساحة المثلث متساوي الأضلاع والقائم
- هناك طرق عديدة لحساب مساحة المثلث قائم الزاوية.
- القانون الشامل لاستنتاج مساحة المثلث: ويعتمد على حساب طول قاعدة المثلث وارتفاعه، ولأن أحد أضلاع المثلث متعامد على الضلع الأخر فإن أحد هذه الأضلاع يمثّل قاعدة المثلث، والضلع الأخر يمثّل ارتفاع المثلث؛ بحيث تكون الزاوية القائمة بين ضلع الساق وضلع الارتفاع تساوي 90 درجة:
- القانون العام: مساحة المثلث = (½)× طول القاعدة × الارتفاع.
- عندما يكون طول ضلع الوتر معلومًا، وكذلك طول إحدى الساقين، فيمكن حساب طول الساق الأخرى عن طريق نظرية فيثاغورس، ثم يتم التعويض في القانون العام.
- نظرية فيثاغورس: الوتر²= الضلع الأول² + الضلع الثاني².
- كذلك عندما يكون طول ضلع الوتر معلومًا وكذلك إحدى الزوايا قياسها معلوم، أو معلوم طول أحد الأضلاع وقياس إحدى الزوايا، فيمكن حساب طول الأضلاع المجهولة عن طريق قوانين جيب (جا)، وجيب تمام (جتا)، وظل الزوايا (ظا)، وهي:
قانون جيب جا (الزاوية)= الضلع المقابل/الوتر.
قانون جيب تمام جتا (الزاوية)= الضلع المجاور/الوتر.
ظل الزاوية ظا (الزاوية)= الضلع المقابل/الضلع المجاور.
مساحة المثلث متساوي الساقين وقائم الزاوية.
- لأن ضلعي ساقي المثلث قائم الزاوية متساويتان، ويمثل أحد هذه الاضلاع قاعدة المثلث، والضلع الأخر يمثل ارتفاع المثلث، فإن القانون يمكن كتابته بطريقة مختلفة كالاتي: مساحة المثلث = (½)×طول الساق².
- معادلة هيرون (Herons formula) إذا كان ضلعا الزاوية القائمة هما (أ، ب) وضلع الوتر هو ج، فإن مساحة المثلث = [س×(س-أ)×(س-ب)×(س-ج)]√
حيث إنّ: س= (أ+ ب+ ج)/2.
شاهد أيضًا: بحث عن المتطابقات المثلثية وإثباتها
أمثلة لمسائل حساب مساحة المثلث
- المسألة الأولى: إذا كان طول ضلع قاعدة المثلث القائم 6 سم، وارتفاعه 5 سم، فما هي مساحته؟
حل المسألة: عن طريق تطبيق القانون: مساحة المثلث = (½)×طول القاعدة × الارتفاع
مساحة المثلث= (½)×6×5 = 15 سم².
- المسألة الثانية: إذا كان طول ضلع قاعدة المثلث 4 سم، وطول الوتر 5 سم، فما هي مساحته؟
حل المسألة: استخدام قانون فيثاغورث لاستنتاج ارتفاع المثلث، وذلك كالاتي:
(الوتر) ² = (الضلع الأول) ² + (الضلع الثاني) ²، وبالتالي:
ارتفاع المثلث² = الوتر² – القاعدة² = 25 – 16= 9 سم.
وبحساب الجذر التربيعي يكون الارتفاع = 3 سم.
استخدام قانون حساب مساحة المثلث القائم بعد استنتاج الارتفاع:
مساحة المثلث القائم = (½)×4×3 = (½) x 12=6 سم².
- المسألة الثالثة: إذا علمت أن طول ضلعي الزاوية القائمة في مثلث قائم الزاوية 10 سم، و0.1 سم، فما هي مساحته؟
حل المسألة: يمثل ضلعي الزاوية القائمة ارتفاع المثلث وطول ضلع قاعدته، وعليه تكون مساحة المثلث تساوي: ½×0.1×10= ½ سم².
شاهد أيضًا: قانون محيط المثلث بالرموز
هكذا شرح هذا المقال عن مساحة المثلث متساوي الأضلاع والقائم، كيفية استنتاج مساحة المثلث متساوي الأضلاع والقائم وكذلك أمثلة على حل مسائل حساب مساحة المثلث.